Bài toán đếm hình của học sinh lớp 6: "Khoai" đến mức người lớn cũng toát mồ hôi, nếu giải được chứng tỏ trí thông minh không vừa

APMOPS là kỳ thi Olympic Toán học, tạo điều kiện cho những thiên tài toán học có cơ hội giao lưu và tranh tài với bạn bè cùng lứa tuổi đến từ khắp các nước trong khu vực châu Á – Thái Bình Dương như: Úc, Brunei, Trung Quốc, Hồng Kông, Ấn Độ, Indonesia, Việt Nam, Malaysia, New Zealand, Singapore, Hàn Quốc, Đài Loan, Philippines.

Kỳ thi APMOPS bao gồm 2 vòng thi. Vòng 1 được tổ chức tại các quốc gia, trong đó có cả Việt Nam. Những thí sinh đạt kết quả cao nhất tại vòng 1 của khu vực châu Á – Thái Bình Dương sẽ được Học viện Hwa Chong mời tham dự vòng chung kết kỳ thi APMOPS tại Singapore. Được biết, đối tượng tham gia kỳ thi là các học sinh dưới 13 tuổi (lớp 6 và lớp 7). 

Dưới đây là một bài toán trong kỳ thi APMOPS 2019 được tổ chức tháng 4/2019. Bạn có thể làm thử để xem khả năng toán học của mình đến đâu:

Bài toán:

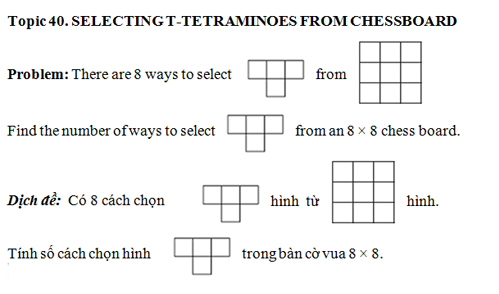
Đáp án:

Tô màu đen - trắng xen kẽ nhau cho 64 ô của bàn cờ vua 8 × 8.

Mỗi hình chữ T gồm có 4 ô với 3 ô cùng màu và có thể chia thành 2 phần:

Phần đầu chữ T gồm 3 ô vuông 1 × 1 và phần đuôi chữ T gồm 1 ô vuông 1 × 1.

Để ý rằng trong bàn cờ vua 8 × 8 có thể tạo ra 6 × 6 = 36 hình vuông 3 × 3.

Do các hình vuông 3 × 3 giao nhau sẽ có các hình chữ T bị trùng lặp nên chúng ta sẽ đếm số các hình chữ T theo 2 bước sau:

Bước 1: Trong mỗi hình vuông 3 × 3 lấy 4 chữ T cùng có đuôi là hình vuông trung tâm 1 × 1. Tổng số cách lấy hình chữ T loại này là 36 × 4 = 144 (cách).

Bước 2: Có 6 cách lấy hình chữ T mà phần đuôi 1 × 1 có cạnh nằm trên 1 cạnh của bàn cờ 8 × 8 (bỏ đi các ô góc bàn cờ). Từ đó có 6 × 4 = 24 (cách).

Kết luận: Do cách lấy các hình chữ T trong 2 bước không bị trùng lặp và hết các khả năng nên tổng số cách lấy hình chữ T trên bàn cờ là: 144 + 24 = 168 (cách).